Transformer-secondary Combination
The combination of transformers, secondary circuit or main, and
the consumers’ services makes up the secondary system. Secondary
systems are predominantly single-phase, except for larger commercial
and industrial consumers, who are supplied from three-phase systems.
While the discussion will be limited to single-phase systems, the principles
and methods employed in their design will serve for other types
of secondary systems.
The number of consumers’ services and their loads, the voltage
drop, the size of conductors, and the spacing and size of transformers
are all variables that are interdependent. They are factors which must
be considered in combination to arrive at a satisfactory design. There
are many theoretical combinations of these factors that will achieve economical
solutions to the problems of design.
For practical purposes, however, these combinations can be reduced
to fewer and more manageable numbers. Certain assumptions
can be made safely:
1. The load can be considered uniformly distributed along a secondary
whose length can be considered fixed. Although not strictly
true, this assumption does represent a majority of conditions, but
concentrated or scattered loads must be considered separately.
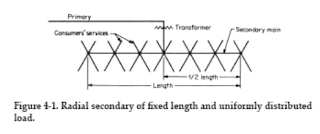
2. The length of secondary circuit is fixed either by geography or by
the type of design; e.g., each city block could be fed by one or more
secondary circuits. Refer to Figure 4-1.
3. In practice, the number and sizes of conductors and transformers
are limited, usually to two or three in number, and to certain standard
sizes because of manufacturing, purchasing, stocking, and
construction economies.
The problem then is to determine the proper combination of conductor
or wire, transformer, and transformer spacing for the least annual
cost, using the materials available while providing for satisfactory voltage
variations, including flicker. Also, the design should consider not
only present loads, but the economics of supplying future loads as well.
Computers permit study of a greater number of combinations.
Conductor Size
It may be well to begin with a determination of the size of conductor.
The maximum demand for each of the consumers is known and a
coincidence or diversity factor, determined by analyses or from previous
experience, applied. Assuming uniformly distributed loads, the loading
on each half of the circuit (each direction from the transformer) can
be expressed as load density in kilowatts per thousand feet or similar
units.
Voltage Drop
For determining voltage drop, the load can be assumed to be concentrated
at the midpoint of the secondary main between the transformer
and the last consumer, i.e., one-quarter of the length of the conductor
from the transformer. The total load connected to one-half the circuit is
converted into a coincident maximum demand in amperes.
A maximum tolerable voltage drop (to the last consumer) is assumed
and divided by the coincident demand in half the circuit,
expressed in amperes. The result will give the maximum permissible
resistance of the conductor. On the basis of its length (one-quarter of the
circuit), the resistance per unit (1000 ft) can be determined. The standard-
size conductor whose unit resistance is equal to or less than that
calculated can be selected.
This assumes the loads are at or near unity power factor; where
this is not so, impedance values based on the spacing between conductors
must be used. Also, the drop in one conductor is calculated,
which assumes no current in the neutral conductor and a load balanced
equally between the two energized or line conductors; where this is not
so, voltage drop in the neutral conductor must also be calculated and
the greater of the drops in the two line conductors used in selecting the
standard-size conductor.
Losses
The next step is to determine the loss in the secondary mains. The
value of current and the unit resistance of the conductor are known; for
the purposes of determining losses, the full load can be considered to be
at one-third the distance from the transformer. This approximate value
in watts or kilowatts is multiplied by an estimate of the “equivalent
hours” duration to obtain the energy losses in watt-hours or kilowatthours.
This should be multiplied by 4 for the entire length of the two
conductors (neglecting the neutral).
It should be noted that while load curves for a particular period
(day, month, year) vary with the value of current, corresponding curves
for losses vary with the square of the current, even though the curves
may have a similar configuration.
Like the load factor, a loss factor is
the ratio of average power loss for a certain period of time (day, month,
year) to the maximum loss or loss at peak load (for a stipulated time:
15, 30, or 60 min) during the same period. This value can be determined
with sufficient accuracy by analysis of a few typical daily load curves
for the period involved. This loss factor always lies between the load
factor (for long, sustained peak loads) and the square of the load factor
(for short, sharp peaks). The loss factor multiplied by 24 equals the daily
equivalent hours.
Returning to the energy losses, in watt-hours or kilowatt-hours,
these are evaluated at the system cost per kilowatt-hour (which includes
not only fuel costs, but carrying charges on equipment, operating costs,
and other overheads). This value is compared with the carrying charges
(including maintenance costs and appropriate overheads) on the installed
cost of the conductors. If the two values are reasonably close, the conductor
selected is economically satisfactory, according to Kelvin’s law.
Kelvin’s Law
Kelvin’s law is generally expressed as follows: The most economical
size of conductor is that for which the annual charge on the investment
is equal to the annual cost of energy loss.
If these two values are not reasonably close, another size of conductor
may be chosen, or the length of the secondary main (and its
connected loads and its coincident maximum demand) may be changed;
and either process may be repeated until the values of annual charges
and annual cost of energy losses are reasonably close.
Transformer Size
Having determined the tentative size of conductor, the next step is
to determine the size of the transformer to be installed. The value of the
diversified coincident demand for the loads connected to the secondary
main having been determined, the nearest standard-size transformer (in
kVA) to the demand (in kW) is tentatively selected. To allow for future
growth and not to prejudice the life of the transformer, the size chosen
is usually larger than the demand.
The most economical load of a transformer is that for which the annual
cost of its copper loss is equal to the annual carrying charges of the
transformer installed plus the annual cost of the core loss. The core loss
can be considered constant regardless of the load carried by the transformer.
Values of core loss and transformer resistance, both expressed as
percentages at full load, vary with the manufacturer, vintage, size, and
other characteristics, and are found in the transformer specifications;
core loss is usually a fraction of one percent, while resistance is usually
less than 2 percent (reflecting the high efficiency of transformers). Here,
too, if the two values are not close, another size of transformer may be
chosen, or the secondary circuit may be changed so that two or more
transformers supply the load. It may be necessary to review the conductor
size and loads for the new resulting circuits.
It is obvious that any secondary-transformer configuration represents
a compromise. Much depends on the relative costs of material
and labor, which may vary widely from time to time and from place to
place. Further, other considerations may play a great part in the final
determination; e.g., conductor sizes may change to meet mechanical
requirements.
Future Growth
To provide for future growth, loads are adjusted upward by a percentage
estimated to represent probable increase over a specified period
of time. Facilities to serve these increased loads are designed in the same
manner described. The difference in investment costs for each design is
evaluated in terms of the future worth of the present increment of cost
of the additional facilities provided for growth. This is compared to the
cost of installing the facilities at the future time. If it is less, it is desirable
to provide for the future load at the time of initial installation. If not,
provision for future load growth should be dropped, or scaled down to
values and timing that will justify some value of additional cost.
To accommodate the load growth, the transformer and conductors
can be replaced with larger ones, or more popularly, the secondary circuit
can be divided into two or more parts without changing conductors;
a suitably sized transformer is then added to the newly formed secondary
circuits. Comparison of costs and annual carrying charges dictate the
method selected.
Networks
The analysis described pertains to radial secondary circuits. Where
networks are involved, the same principles and methods can be applied
by assuming the network to be divided into a number of adjacent radialtype
circuits, as shown in Figure 4-2; no appreciable error is introduced.
The general principles and methods applied to overhead singlephase
radial-type secondary circuits may be applied to underground
circuits and three-phase three- or four-wire circuits by proper adjustment
of terms to fit the cases. With underground circuits, the lesser current-
carrying capacity of a size of conductor, without overheating, must
be taken into account. In network design, the ability to burn clear the
conductors in the cable under fault or short-circuit conditions should
also be ascertained. These additional considerations may be taken into
account after the economic studies are made.
Rural Systems
Where consumers are scattered, such as in rural areas on in the
case of three-phase consumers in an area supplied essentially at single
phase, the load may be served either by extending the secondary from
one transformer or bank of transformers, or by installing a separate
transformer or transformers to serve those consumers. Annual carrying
charges, including costs of losses, should be compared in selecting the
method of supply.
There are many other problems in the design of secondary systems,
but they lend themselves to the application of the same basic principles
and methods, with proper consideration given to their particular requirements.